NASCAR

In the previous article on NASCAR exhausts 12 months ago, the subject of materials was discussed without addressing the design of the exhaust system itself. The NASCAR regulations offer very specific guidance to the teams about the design and configuration of the exhaust system. The exit of the exhaust at the sides of the race car are of particular interest. The perimeter of any pipe in the exhaust is mandated to be 13.25 in (336.5 mm), but at the exit of the system, which in NASCAR is along the side of the car, it is unrealistic to accommodate a circular-section pipe that equates to this circumference. Moreover, NASCAR's rules prohibit this, as they mandate a maximum pipe diameter of 4 in (101.6 mm). A 4 in pipe has a perimeter of 12.56 in (319 mm) so the perimeter rule can only apply to sections of the exhaust that are non-circular.

There is also specific guidance for the exits of Sprint Cup exhausts regarding height, which should be a minimum of 2 in (50.8 mm) except for exhausts used at Daytona and Talladega. So, we can expect to see a very flattened exit to the exhaust. This flattened exhaust system is desirable as it allows the car to run low.

So, what are the implications of running flattened sections of pipe in the car? The pressure losses in a length of straight pipe are dictated by the fluid within, its flow rate, Reynolds number and the geometry of the pipe. The minimum pressure loss in the pipe is achieved where the cross-section of the pipe is circular. Take the example of a 4 in diameter pipe; this has a cross-sectional area of 12.56 sq in . If we turn this into a simple rectangular section of 2 in by 6.28 in, the pressure losses in the pipe are the same as would be found in a circular pipe of just over 3 in.

The concept that gives us this relationship between pipe geometry and effective diameter is that of 'hydraulic diameter'. The hydraulic diameter of any duct is defined as four times the cross-sectional area divided by the perimeter.

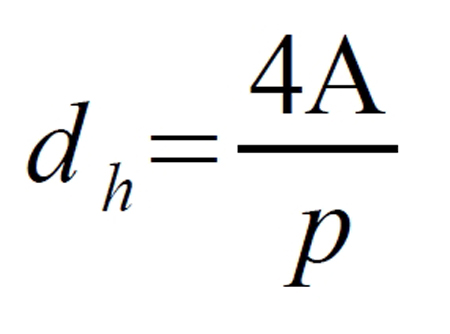
Where:
dh = hydraulic or effective diameter
A = cross-sectional area
p = perimeter

For a circular section, the diameter and the hydraulic diameter are equal.

For a given height or section, say 2 in, the increase in hydraulic diameter with increasing section width is a matter of diminishing returns. If we were able to run an exit twice as wide - that is, 2 in x 12.56 in - the hydraulic diameter is increased to only 3.45 sq in, an increase of only 15% for a doubling in area. If, however, we keep the 6.28 in side and increase the height to 4 in, we find that the hydraulic diameter increases to 4.88 sq in.

The pattern here is that there is a definite advantage to running rectangular pipes of certain aspect ratio, as in the ratio of the lengths of the sides. Within the rules that NASCAR mandates, and within the packaging constraints of the car, there is much scope for experiment. One problem with rectangular sections with two short sides and two long sides is that they often require 'bracing' from top to bottom. In terms of hydraulic diameter, this has some interesting effects. Sharpen your pencil and see what you find.

Fig. 1 - In NASCAR Sprint Cup, the exhaust exits between the front and rear wheels. We can't see the exhaust exit directly, but we can be sure that it has been well engineered

Written by Wayne Ward