Electric motors
Although many racing series restrict engine performance by imposing intake air restrictors, such as Formula Three or the various endurance series and the Le Mans race, others are a fixed maximum displacement, such as MotoGP, NASCAR and Formula One. The race for greater power means a relentless drive for higher engine speeds. Fixed torque (assuming a certain level of volumetric efficiency and natural aspiration), thanks to fixed displacement, means that increased power comes about through higher engine speeds. Torque, multiplied by speed, equals power, but engine torque is anything but constant. Race engines are optimised over a certain speed range, and even over this relatively narrow band, torque varies markedly.
Electric machines, whether used for direct propulsion or, as is the case with hybrids, to augment the conventional internal combustion engine, are essentially constant-torque machines. Unaffected by the vagaries of unsteady airflow and without the headache of keeping hundreds of mechanical components working in harmony, a wonderful plateau of torque remains undiminished, so long as the motors' power electronics switch power in their electromagnets at the optimum timing. Electric motors, unencumbered by heavy battery packs, would make a wonderful propulsion system for a car or motorcycle. If power is your target, and you also seek low motor mass, then rotor speed is your friend. For a given motor geometry and construction, power is directly proportional to speed.
If we ignore the actual electrical operation of the motor - which I imagine will please the mechanical engineers here - let us see how the rotor geometry affects torque. The tangential force per unit area of the rotor, acting on the rotor, is a function of the current density in the windings and the flux density in the gap between the rotor and the stator. The first quantity is a measure of the current being used, the second is a measure of the strength of the magnets and the gap between the rotor and stator.
The torque per unit area of rotor is the product of the tangential force, F, and the rotor radius, r, such that:
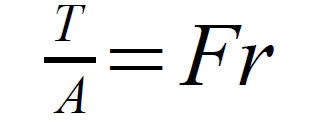
and from this it follows that torque is the product of the tangential force per unit area, the rotor radius and the rotor surface area.
For a rotor of radius r and axial length, l:
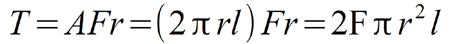
In seeking high torque, rotor length is important, but rotor radius is a much more potent performance factor. However, as is the case with crankshaft stroke and increased engine speeds, large rotor diameters and high rotor speeds are not easy bedfellows. Even if we assume that the rotor avoids any resonant conditions throughout its running range, centrifugal forces are a function of the rotor radius and the square of the rotor speed. In trying to remain within the mechanical strength constraints of the rotor materials, we have to play speed against rotor radius. Increasing rotor length to increase torque is reasonably efficient, but there are limits to this as well, owing to shaft dynamics. As with an engine, so there are compromises to be made with electric motors.
With comments made in the press recently about the new 2014 Formula One power units, which have an electric motor integral with the turbocharger and which will run at or around 100,000 rpm, choosing the correct rotor dimensions in order to give the correct performance while not failing under centrifugal loading will be no easy matter.
Written by Wayne Ward