Tightening using torque and angle

In the previous two articles on the subject of fastener tightening, we looked at two methods of pre-loading threaded fasteners - torque control and the turn-of-nut method.

The method of torque tensioning remains a favourite; anyone with a torque wrench can use this method, but a lot of engineers are wary of it because of the variability of factors that influence the load. Friction is the main variable; it changes with materials, surface finish, lubricant, and is often worryingly inconsistent, even when we believe we have good control over all of the above. The application of lubricant or thread-locking compounds is a manual process, and variability is unavoidable. Therefore, even using the same tool, the operator is a variable.

The turn-of-nut method also has a couple of limitations. There is no torque developed until the nut is in contact with its adjacent joint member (ignoring 'prevailing torque' fasteners) and when we do have contact, there is a very non-linear portion of the angle-load curve. The first limitation can very easily be overcome, but the second cannot be avoided, as the turn-of-nut method is not accurate enough without detailed knowledge of the non-linear portion of the angle-load curve. Given that the non-linear behaviour is due in part to geometric inconsistencies, we cannot be sure we properly understand how the joint behaves in all circumstances.

All is not lost though. We can combine the torque tensioning and turn-of-nut methods to arrive at a more reliable process for pre-loading fasteners. In combining the two methods, we initially use torque control to take us just beyond the non-linear portion of the angle-load curve and onto the elastic part of the curve. The load induced in the fastener during the initial torque tensioning is modest in comparison to the final load that will be developed, and because the load is low, any effect from geometric inconsistencies or friction in calculating the load at the end of the torque stage is small enough not to cause too many worries.

Hereafter, we return to our turn-of-nut method. We are in the linear elastic portion of the angle-load graph for which we have measured or calculated data, and providing we can accurately measure the angle through which the nut is turned, we can be pretty sure we have got as close to our desired pre-load as it is possible to be using conventional tools.

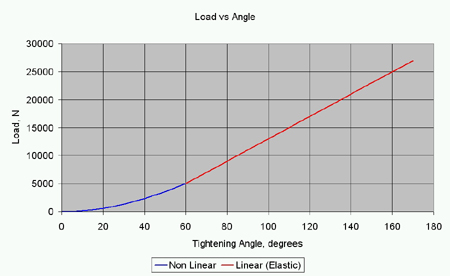
Fig. 1 illustrates the method. Let us say that we want to induce a load of 25,000 N in the fastener. The linear elastic portion of the graph extends to a point where the load is 5000 N. We select a torque to take us just beyond this point, say 6000 N. For torque tensioning, ±20% accuracy might be reasonable, so the load could be 4800-7200 N. If we then tighten the bolt by 95º, the load should be 23,700-26,200 N. This is a range of 5.2% below target to 4.8% above.

For normal toque tensioning, we might expect a range of 20,000-30,000 N. If we can gain an understanding of the non-linear behaviour of the joint and the gradient of the elastic portion of the graph, we can predict bolt pre-load with a high level of accuracy.

Fig. 1 - Load-angle graph, showing non-linear and linear elastic behaviour

Written by Wayne Ward